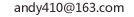高数书上数列极限例题2,如下不懂求帮助!
将分母改成一样的 那么所有的项都可以合并 这样就可以得出分子1加到n等于n(n+1)/2
虽然你没给出定理3的内容,但从这个证明中的描述可以看出,定理3应该是这样的:
如果一个数列{Xn}的极限a满足:a<0(或a>0);那么{Xn}必然从某项开始有:Xn<0(或Xn>0);
而这个推论,(基本上)就是定理3的【逆命题】。本来,对于普通的命题,其逆命题是未必为真的。但定理3实在很特殊:
它同时对(a<0)和(a>0)进行判断,这就(基本上)相当于同时肯定了一个命题和它的【否命题】;而我们都知道,【逆命题】和【否命题】互为【逆否命题】,它们是等价的。
虽然这里我所说的逆命题、否命题都不是严格的,但这些特点就为该推论的成立提供了基础条件。
定理3和推论中,都假定极限存在。所以,可以定义以下命题:
①:a>0;
②:a<0;
③:a≥0;
④:a≤0;
⑤:a=0;
它们的关系是:
(1)①、②、⑤两两相互对立;——所谓对立,就是不能同时为真;
(2)①、④相互矛盾;——所谓矛盾,就是不能同时为真,也不能同时为假;
(3)②、③相互矛盾;
(4)③、④相交于⑤;
而关于Xn的判断,都是针对n大于某个项数后的所有项而言的。具体包括以下命题:
Ⅰ:存在N1:若n>N1,则Xn>0;
Ⅱ:存在N2:若n>N2,则Xn<0;
Ⅲ:存在N3:若n>N3,则Xn≥0;
Ⅳ:存在N4:若n>N4,则Xn≤0;
Ⅴ:存在N5:若n>N5,则Xn=0;
Ⅵ:不存在N6,使得当n>N6时,Xn与0有固定统一的大小关系;
它们的关系就是解决你的问题的关键:
(1)Ⅰ、Ⅱ、Ⅴ相互独立;
(2)Ⅰ、Ⅳ相互独立;
(3)Ⅱ、Ⅲ相互独立;
(4)Ⅲ、Ⅳ相交于Ⅴ;
(5)Ⅰ~Ⅴ的选言命题,与Ⅵ相互矛盾;
上面所说的N1~N5,对单个命题而言,我们可以换用任何字母来表示这个整数,我之所以用五个不同的符号表示,只是为了表达这样一个意思:这五个命题中所说的五个整数,可能不相等。以证明中用到的Ⅱ与Ⅲ的对立关系为例说明:
n大于N2和N3,是Ⅱ与Ⅲ分别成立的条件。如果令N=max{N2,N3},即:N为N2和N3中【较大】的那个(显然,这样的N是一定存在的——只要N2和N3存在);那么,因为N2和N3都可以分别令Ⅱ和Ⅲ为真,所以,比它们更大的N,肯定更可以令Ⅱ和Ⅲ为真了。此时,就有了这样的结论:
Ⅱ′:当n>N时,Xn必然小于0;
Ⅲ′:当n>N时,Xn必然不小于0;
这显然是相互矛盾的。本题中的证明,就是利用这个矛盾进行反证的。
我们可利用上面定义的各个命题,重写证明过程:
定理3可以表示为:
①→Ⅰ;②→Ⅱ;
而所需证明的推论可以这样表示:
Ⅲ→③;Ⅳ→④;
那么证明就是这样的:
如果:Ⅲ→③不成立;那么就有:Ⅲ为真,且③为假;
③为假,所以它的矛盾命题②,必然为真;
那么根据:②→Ⅱ,可得:Ⅱ为真;
但Ⅱ与Ⅲ矛盾;由此可证明Ⅲ→③必然成立。
上面是反证法,其实还可以用直接法:
若Ⅲ为真,则Ⅱ为假;——对立命题的性质;
若Ⅱ为假,则②为假;——逆否命题的性质;
若②为假,则③为真;——矛盾命题的性质;
转换成原来的命题,就是:
如果:存在N,使得n>N时,Xn≥0;
那么:就不存在N,使得n>N时,Xn<0;
如果:不存在N,使得n>N时,Xn<0;
那么:{Xn}的极限a就不满足:a<0;
如果:{Xn}的极限a不满足:a<0;
那么:{Xn}的极限a就一定满足:a≥0;
对ε可以限制上界但不能限制下界,比如ε<1,ε<1/2等等,这不影响其“任意小”的特质,也可以这样理解,那就是对于一个小一点的ε都可以找到N,那么ε大一点时,还取原来的N,还是能保证|Xn-a|<ε。
对于N,当|Xn-a|很简单时,可以直接由|Xn-a|<ε求出n>N;否则可以先对|Xn-a|放大,放大为一个与n有关且简单的式子,比如放大为1/n的倍数,本题可得|Xn-a|<1/n,由这个式子小于ε来确定N。
对于本题来说,如果选择|Xn-a|<1/n,那么ε也不用限定小于1,过程如下:
因为|Xn-a|<1/n,所以对于任意小的正数ε,要使得|Xn-a|<ε,只要1/n<ε,即n>1/ε即可,选择正整数N=[1/ε],则n>N时,恒有|Xn-a|<ε。所以数列{Xn}的极限是0。
这种写法不必要,书上这样写有两个原因:
1、这样写求出的ε形式比较简单;
2、要我们知道,在做一些较复杂问题时,可以对|Xn-a|的结果做适当的放大,有助于解出结果。
做为本题,由于比较简单,不做这种放大也是可以的。
答:lim(n→∞)x(n)= a <==> 对任一 ε>0,存在 n∈z+,当n>n时,有 |x(n)-a| <ε <==> 对任一 ε>0,存在 n∈z+,当n>n时,有 x(n)∈ (a-ε,a+ε)<==> 对任一 ε>0,存在 n∈z+,至多肌花冠拘攉饺圭邪氦矛只有 n = 1,2,…,n 不满足 x(n)∈ (a-ε,...
答:若n=2k-1 2·k-1>N=2K 解得,k>K+1/2 若n=2k 2·k>N=2K 解得,k>K
答:题目解答要应用”单调增加有上界的数列一定有极限“这个定理。为此要验证定理条件。这个划线的结论就是函数有上界。加上下面再验证增加,就完全验证了定理条件。就可以得到数列有极限的结论了。
答:1-1/n²可化成(n+1)(n-1)/n²,每一项这样化解,约分剩(n+1)/2n,n趋向正无穷时等于1/2。平方差公式展开。然后交换合并把和部分相乘,差部分相乘。数列极限用通俗的语言来说就是:对于数列an,如果它的极限是a,那么,不管给出多小的正数ε,总能找到正整数N,只要数列的下标n>...
答:lnL =lim(n->∞) [1/(n+1) ] { ∑(i:1->n) ln[(n+i)/n ] } =lim(n->∞) [1/(n+1) ] { ∑(i:1->n) ln[(1 + i/n) } =∫(0->1) ln(1+x) dx =[ xln(1+x) ]|(0->1) -∫(0->1) x/(1+x) dx =ln2 - ∫(0->1) [1- 1/(1+x)...
答:2Xn+2+Xn+1=2Xn+1+Xn 2Xn+1+Xn=2b+a.(1)由Xn+2=(Xn+1+Xn)/2得 2(Xn+2-Xn+1)=-(Xn+1-Xn)Xn+1-Xn=(b-a)(-1/2)^(n-1).(2)(1)-(2)×2得:Xn=[(2b+a)-2(b-a)(-1/2)^(n-1)]/3 当n→∞时Xn→(2b+a)/3 所以,数列{Xn}收敛,其极限为(2b+a)/3...
答:由于两个数列中的相对应的两项之比收敛于常数e,所以当n足够大时,un 近似于vn的e倍。由于当n不断增大时,un任意地接近于0,所以vn也任意地接近于0,即数列(vn)的极限=0。2. 对于任何给定的正数e,存在N,使得任何大于N的 k 都有|ak-a|<e/2 注意,对于给定的N,|a1+a2+...+aN-Na|...
答:当n→+∞时,原式=∫[1/√(4-x^2)]dx,从0积到1。显然此积分是存在的,原题极限的值就是此积分的值。令x=2sinθ,积分区间对应的变为0→π/6 带入积分式中有∫[1/√(4-x^2)]dx=∫[1/√(4-4(sinθ)^2)]d(2sinθ)=∫dθ=π/6-0=π/6 所以,原数列的极限存在,为π...
答:L=lim(n->∞)[(2n)!/(n!.n^n)]^[1/(n+1)]lnL =lim(n->∞)[1/(n+1)]{∑(i:1->n)ln[(n+i)/n]} =lim(n->∞)[1/(n+1)]{∑(i:1->n)ln[(1+i/n)} =∫(0->1)ln(1+x)dx =[xln(1+x)]、(0->1)-∫(0->1)x/(1+x)dx =ln2-∫(0->1)[1-1...
答:①0 已知n为正数,当n为奇数,结果等于0,当n为偶数,结果也等于0。综上,结果为0。②1/2 已知n为正数,当n无穷大的时候,自然数+1和-5可以忽略不计,结果为n/2n,即是1/2。综上,结果为1/2。③0 由题可知,n为正整数,当n无穷大时,分母无穷大,结果为0。综上,结果为0。